学生时代一定都学过圆周率,在一些题目也常见与圆相关的计算。小小的圆圈,可以说隐藏了不少的奥秘,圆周率的背后更是充满了不少故事。
6月8日
谷歌云发布了一项消息:计算机学家Emma Haruka Iwao通过谷歌云的计算引擎,将圆周率计算到了100万亿个小数位,并打破了2021年瑞士科研团队创下的小数点后62.8万亿的纪录。
1761年德国数学家兰伯特就证明,圆周率是一个无理数,即无限不循环小数。那么既然知道算不尽,还动用超级计算机进行计算有什么意义呢?
假如有一天圆周率被算尽了,对数学乃至整个物质世界又会有什么样的影响?
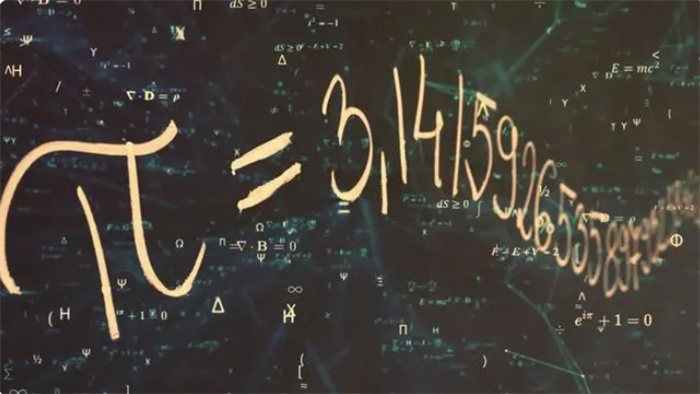
圆和我们的生活息息相关
对圆周率的计算,早在数千年前的古人就开始探索方法了,最初他们估算出圆周率的近似值应该是3,但随着技术进一步发展,对圆周率的精度也提出了更高的要求。
公元前2世纪,古希腊数学家阿基米德通过迭代算法和两侧数值逼近的理念,求出圆周率的下界和上界分别为223/71和22/7,最后取了他们的平均值3.141851为近似值,可以说阿基米德开创了人类历史上通过理论计算圆周率的先河。
公元263年,中国数学家刘徽首次使用求极限的割圆术计算圆周率,得出3.14的数值,但他发现还是偏小,最后割圆到1536边形,求出了3072边形的面积,精确到了3.1416才满意。
公元480年南北朝时期,数学家祖冲之进一步优化了割圆术,计算出圆周率介于3.1415926和3.1415927之间,准确到小数点后七位的精度让祖冲之在后来的800年内都领先世界
虽然割圆术的思路很巧妙,但计算量非常大,越精准的数值意味着越巨量的计算,在没有计算器的情况下,这样的计算难度也颇大,直到十六世纪一些数学家发现圆周率可以用无穷数列的和或者积表示,圆周率的计算一下子就变得简洁明了了。
有了无穷数级的加持后,只要计算的项数越多,得到的圆周率数值就能越精确,但无穷数级就像它的名字一样是算不尽的,这也就引出了另一个问题:
圆周率的数值有尽头吗?
1761年,德国数学家兰伯特利用函数和特殊的函分数,证明了圆周率是一个无限不循环小数,即无理数,除了无理数的特性,德国数学家林曼还证明了圆周率是一个超越数,即圆周率的平方也是无理数,因此圆周率不能作为有理系数多项根的实根。
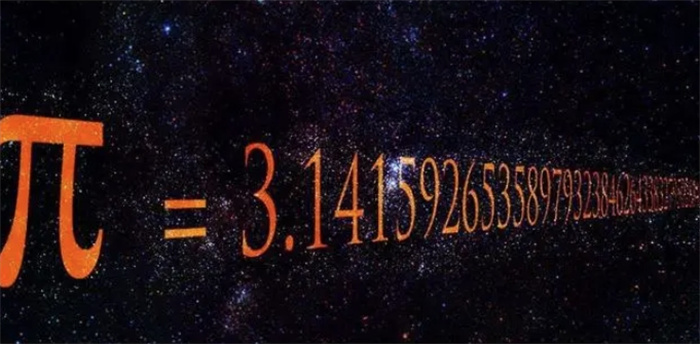
既然明知道圆周率是算不尽的,为什么还要计算下去?
在常见的科技领域中,最多只会用到圆周率小数点后面的几十位,假如要计算当前的可观测宇宙面积率,只要用到圆周小数点后40位,就能把误差缩小到一个氢原子的大小。
所以计算到小数点后几十万乃至上百万位,从实用性来看没有什么意义,继续计算的原因,一方面是因为人类总乐于挑战,试图创造一些新的纪录,不断突破自我超越极限,就像人类虽然现在已经普及了汽车,但相关田径比赛仍然存在。
另一方面,庞大的计算量也可以检验超级计算机性能。比如这次谷歌云计算到百万亿位用了157天23小时31分钟,而2019年31.4万亿位则用了121天,足以看出计算能力的进步。
假如有一天圆周率被算尽了,在排除计算机故障以及其他外在因素后,只能说人类的数学体系出了大问题,理论从来不是单独存在的,所以一旦圆周率被发现不是无理数,则会牵一发而动全身。
首先假如圆周率有尽头,就证明它是一个有理数
但现今的数学理论建立在圆周率是有理数的基础上,微积分就要率先遭遇危机,再而数学大厦也会蒙上阴云,同时不少物理公式也带有圆周率,比如爱因斯坦的引力方程,它描述了时间和空间的关系。

假如圆周率出了问题,就意味着我们所存在的宇宙可能并不是我们认知的那样,欧氏几何也不再适用,圆周率将以一个变量的身份的出现。
但以目前的状况来看,圆周率应该不会被算尽的,它是我们这个宇宙的基本法则,其实圆周率也没有那么神奇,在不同几何方向上,圆周率是不是无理数要依据具体的情况,比如在非欧几何里的罗氏几何和黎氏几何上,圆周率就不是一个定值。
其实圆周率不仅用在基础的理论上,还用在一些保密工作上。比如在社交平台和常用网站上,我们设置的密码还是会有一定逻辑和规律,和我们自身相关。
对于一些极其机密的信息和资料,则需要确保密码是完全无规律的,圆周率就是天然无规律的无穷数,因此常常被当作安全性极高的密码使用。