非欧几何认为一条直线只要够长就会弯曲。一直以来,我们都被告知在同一平面内永不相交的两条直线叫平行线。但事实上,这只是欧几里得几何中的理论,主要适用于我们的日常生活。除此之外,还有非欧几何一不同于欧济里德几何学的几何体系,主要包括罗氏几何和黎曼几何。
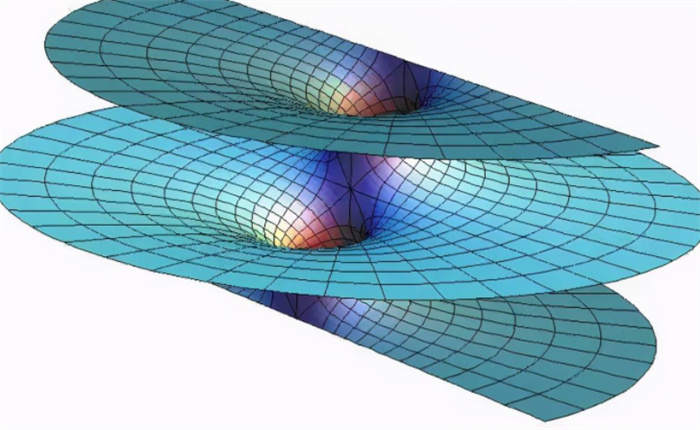
圆弧线
非欧几何最大的不同在于其所考虑问题是基于空间,虚率不为零的平面来进行。要理解所谓的非欧几何中平行线相交,可以从球面上进行简单理解,取球面上任意两点,我们会发现该球面上这两点间最短的距离是其大圆的裂弧部分。这里所说的大圆指的是,在经过球型的平面是所取得的一个圆形,劣弧的意识是这个球型两个点之间最短的那个圆形户县,因此球面上只有大圆是直线。
黎曼几何
以经线和纬线为例,经线都是直线,而纬线中除了赤道之外都不是直线。如果说赤道的大圆是直线,那么应该所有的经线都因该是平行,但是我们知道经线又都在南北极都相交。所以平行线在远处是相交,或者说球面上的所有直线都相交,而这是黎曼几何的假设。
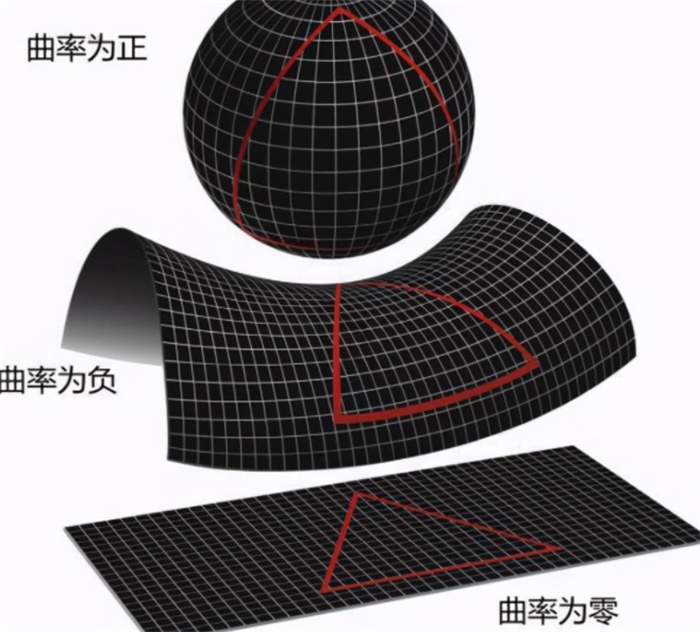
弯曲的直线
欧几里得几何适用于曲力为零的情况。黎曼几何研究的是正曲率空间,而罗氏几何是负曲率空间,曲面是普遍存在的情况平面是曲面的一种特例。在两条直线相交的情况下,再往前衍生一段距离后截取其中的一小段,这样又恢复了平行。如果是从宇宙这样大的角度来看的话,哪怕是直线也是会有弯曲,既然会有弯曲,那就有相交的可能。