在旋转黑洞能层中静止的物体是超光速的。这句话听起来是相当矛盾的:物体怎么可能既静止又超光速呢?为了理解这句话背后的真实情况,我们还得从基础说起。
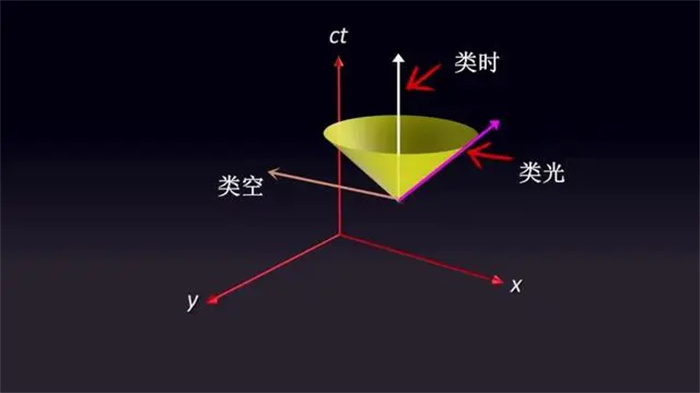
类时、类光和类空
在20世纪之前,人们认为时间是脱离三维空间的独立维度。在三维空间中,不管坐标系是如何选取的,两个固定点的距离是恒定的,我们可以用如下公式表示:ds²=dx²+dy²+dz²。
后来,闵科夫斯基提出,洛伦兹变换是由三维空间和一维时间所构成的四维时空的变换。从此,单独的空间和单独的时间便不复存在,而只有二者的结合才是一项真实的存在。为了纪念他,人们把狭义相对论中的四维时空对应的几何叫作闵科夫斯基几何。
在闵科夫斯基几何中,两点之间的距离不再是一个不变的值,取而代之的是两个事件之间的时空间隔,我们可以用公式表示: ds²=-c²dt²+dx²+dy²+dz²。与三维空间中的距离不同,时空间隔ds²不仅可以是正数,也可以是负数和零。
使ds²<0的区域是类时的,这是一个不必超过光速就可以到达的区域,两个事件之间可以有因果关系;使ds²=0的区域是类光的,在这个区域当中只能以光速运动,两个事件之间只能有一种因果关系;使ds²>0的区域是类空的,这是一个只有超光速才能到达的区域,事件之间没有因果关系。
克尔-纽曼黑洞
在爱因斯坦发表广义相对论不久,史瓦西就得到了第一个解,我们称之为史瓦西解。但史瓦西解是比较简单的,只和质量有关。后来,又有物理学家把带电量也加入进去,得到了带电施瓦西解,或称为R-N解。1963年,克尔考虑了旋转的情况,得到了克尔解。后来,纽曼等人把克尔解推广到带电的情况,得到了克尔-纽曼解。在G=C=1的自然单位制下,我们可以把它写成如下形式:
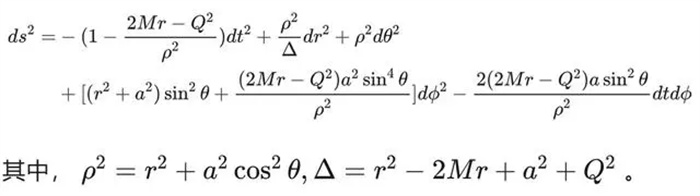
从这个公式我们可以看出,它由质量M、电荷Q和角动量J这三个参数所决定,角动量J是以单位质量角动量a=J/M来表示。当角动量为零时,它会退化成R-N解;当电荷为零时,它会退化成克尔解;当角动量和电荷为零时,它会退化成史瓦西解。

从上图两个式子我们可以看出,无限红移面和视界并不像我们所熟悉的史瓦西黑洞一样是重叠的。在无限红移面和视界之间,就是所谓的能层:外无限红移面和外视界之间是外能层,内无限红移面和内视界之间是内能层。此外,内外两个视界之间的区域是单向膜区,进入此区域的物体将不可避免向内部落去。
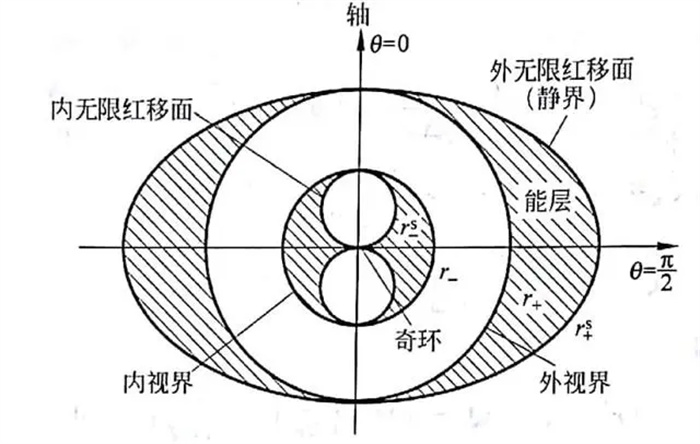
拖拽效应
现在,我们考虑一个在克尔-纽曼时空中静止的物体。此时,dr=dθ=dΦ=0,我们可以将克尔-纽曼解写成以下形式:

事实上,物体在无限红移面和能层中会被迫转动,而这种转动是旋转黑洞的引力场所拖动的。因为无限红移面是时空中物体可静止和不可静止的一个边界,所有它也被叫作静界。